A MATEMÁTICA PODE SER DIFERENTE?
Remo Mannarino
Introdução
Apresento neste livro três entendimentos matemáticos contrários ao senso comum:
(1) Números são neutros: não há números positivos, nem números negativos. Expressões numéricas entram nos cálculos, não os números isoladamente considerados, e o fazem mediante permissão da aritmética, da álgebra, da geometria ou da ciência.
(1) Números são neutros: não há números positivos, nem números negativos. Expressões numéricas entram nos cálculos, não os números isoladamente considerados, e o fazem mediante permissão da aritmética, da álgebra, da geometria ou da ciência.
(2) É
preciso aprender a multiplicar. A ordem dos fatores altera o produto e não
existe a figura do “menos por menos dá mais”. Posso multiplicar uma medição por
outra medição, mas não posso multiplicar uma contagem por outra contagem.
(3) Equações
são torneios horizontais, com “x”, mas sem “y”. As equações verdadeiras são do
primeiro grau e têm uma única incógnita. A estranha equação do segundo grau é
exceção, pois tem, em dois contextos diferentes, uma versão falsa, com duas
raízes, e uma versão verdadeira, mas lúdica, com duas incógnitas. A propósito,
não há equações preestabelecidas, nem gratuitas.
Durante dez
recentes meses estive percorrendo os fundamentos da matemática em regime de
dedicação total, pelas razões que apresentarei no decorrer desta Introdução. A
bem da verdade, foi a primeira vez que entrei de corpo e alma no estudo da
matemática, da qual por sinal estava afastado havia mais de cinquenta anos. E
desta vez eu o fazia sem amarras ou preconceitos de nenhuma natureza.
Sempre
suspeitei que o número é uma ferramenta neutra, sem nenhum sinal, ou melhor, que
não há números “positivos” ou “negativos”, muito menos números “imaginários”, consubstanciando
um entendimento que nunca tivera coragem de enfrentar, porque em oposição frontal
à matemática que aprendi nos livros. Além disso, especular sobre essa hipótese
ousada seria tarefa para profissionais especialistas do ramo, não para mim, que
nem sou matemático.
Desta vez, porém, agindo de modo diverso,
decidi assumir a premissa de que números realmente não têm sinais e com esse
entendimento durante meses dediquei-me com exclusividade absoluta à tarefa de
examinar expressões numéricas, contagens, somas algébricas, multiplicações,
equações e polinômios.
Colhi na
empreitada resultados que me parecem surpreendentes, e nutro, com humildade, a
ambição de que venham a ser examinados por estudiosos da matemática.
Há, com
efeito, dois tipos de contagens, a saber, contagens de módulos, isto é, de
“coisas”, e contagens numéricas ou abstratas (isto é, de posições ou de “vezes”),
com finalidades matemáticas diferentes.
As contagens, não os números, são positivas ou
negativas.
Uma contagem negativa é a imagem de uma contagem
positiva.
As imagens das contagens explicam, nas suas
inter-relações, a metáfora do “menos por menos dá mais”, o que também pode ser
explicado geometricamente.
Nas contagens só o multiplicador multiplica, isto é,
a ordem dos fatores altera o produto.
Equações envolvendo contagens são necessariamente do primeiro grau, com uma única incógnita. As equações de números isolados podem ser de qualquer grau, mas, com mais de uma incógnita, só conheço até agora a equação do segundo grau.]
Percebi que
há na matemática o equívoco de considerar um polinômio igualado a zero como uma
equação. Um polinômio é uma soma algébrica, função de uma variável “x”, que
define um total diferente a cada valor arbitrariamente atribuído a “x”;
igualado a zero, o polinômio indica o ponto da curva representada em gráfico
cartesiano em que a soma algébrica se anula. Por seu turno, uma equação é o confronto de
duas somas algébricas, obrigadas a serem iguais, e serve ao cálculo do valor de
uma contagem, não à localização de um ponto.
Ou seja, há equações, que calculam contagens, e
falsas equações, que localizam pontos. Equações com enredo, concretas, e
equações sem enredo, abstratas.
Tentarei
explicar tudo isso neste livro. Antes, porém, devo revelar o motivo do meu
interesse tardio pelos fundamentos da matemática. Foi uma tentativa, meio pretensiosa
e sobretudo amadora, de resgatar os estudos do professor Astyages Brasil da
Silva, falecido em setembro de 2017. Trata-se de um amigo da época
universitária, profundo conhecedor de geometria descritiva, que me afirmou
repetidas vezes haver construído uma nova matemática, além de me fazer comentários
que deixavam transparecer seu desapreço pelo que chamava de “modelo matemático
atual”.
Tanto quanto
pude saber e perceber, ninguém tomou conhecimento dessa matemática alternativa,
que o mestre só revelaria mediante patrocínio ou no âmbito de algum contrato
remunerado, que jamais logrou conseguir.
Afirmava,
por exemplo, que tinha um novo conceito de número negativo, que “menos por
menos dá menos”, que “uma equação do grau “n” pode ter mais de “n” raízes ou
menos de “n” raízes”, que (-5)² = -25, que a
imagem de “x” é “x-2x”.
Comecei a pesquisa
pelas equações do primeiro grau. Foram tentativas exaustivas. Não cheguei ao
modelo procurado, cujos fundamentos não consegui minimamente alcançar. Paralelamente,
o engenheiro Sandoval Amui decidiu, como eu, pesquisar os fundamentos da
matemática à luz dos comentários do professor Astyages, que lhe foram por mim repassados.
Nessa empreitada, Amui, sobretudo interessado na geometria, acabou
desenvolvendo importantes e inovadores estudos sobre o Teorema de Pitágoras,
para o qual apresentou uma generalização, e construiu uma demonstração da
Conjectura de Fermat, simples e convincente, conforme apresenta no livro “A
Circunferência, Pitágoras e Fermat”, publicado em novembro de 2019 pela Editora
Catalivros. Mas não conseguiu, igualmente, nenhuma pista do modelo de Astyages.
Decidi
então assumir a minha velha hipótese de que não há números negativos, e o
esforço de muitos meses me rendeu as percepções que acima mencionei. Atirei no
que vi, acertei no que não vi, o que me levou a publicar em julho de 2019 o
livro “Reflexões de um matemático acidental”, com a pretensão de ver esses
entendimentos examinados, mesmo pressentindo que o livro não despertaria nenhum
entusiasmo ou interesse.
Afinal, sou
um assumido não-matemático desconhecido.
A
indiferença com que o livro foi recebido confirmou o pressentimento: não tive
nenhum retorno ou comentário, nem para o bem, nem para o mal. Reconheço, porém,
que dificilmente poderia ter sido de outra forma, pois o livro não primou pela
organização, nem estava otimizado didaticamente.
Escolhi não
desistir e por isso aqui retorno com este segundo livro, que escrevi com a
finalidade de reiterar e ampliar os mesmos entendimentos, desta vez seguindo um
roteiro e com um texto que me parece apropriado. Também corrijo algumas
imperfeições do livro anterior e adiciono uma explicação completa sobre a
equação do segundo grau, após introduzir o conceito de “falsas equações”.
Este novo
livro tem poucas páginas, mas sua leitura pode não ser atraente, pois sobretudo
voltado para conceitos e definições.
Acredito em tudo que nele escrevi, pois resume minha
nova percepção da matemática. Sei que posso estar enganado, talvez muito
enganado. Seja como for, minha intenção é contribuir de alguma forma para o
progresso da matemática.
Remo Mannarino
CAPÍTULO I – OS
ENTENDIMENTOS APRESENTADOS NESTE LIVRO
O número é uma ferramenta neutra,
nem positivo, nem negativo.
O número, isoladamente considerado,
informa uma magnitude, mas a forma de usar uma expressão numérica depende da
natureza do que está sendo por ela quantificado e da aplicação matemática a que
se destina.
A expressão numérica entra nos
cálculos, não o número em abstrato, e ela o faz mediante uma autorização, seja
da aritmética, da álgebra, da geometria ou da ciência.
“Número positivo” e “número
negativo” não são números, mas expressões numéricas de contagens. Não tem
nenhum sentido, por exemplo, elevar um “número negativo” ao quadrado ou extrair
a raiz quadrada de um “número negativo”.
O que importa é a informação
numérica, não propriamente o número. Um número, isoladamente considerado, é
como um verbo no dicionário, ali acantonado, sem sujeito e sem complementos, a
informar uma ação sem dizer quem, onde, como ou quando.
Sobre medir, contar e
multiplicar
Medir (tanto quanto pesar ou
aferir) é comparar. Mede-se (pesa-se ou afere-se) para a geometria e para a ciência.
Contar, porém, é diferente.
Conta-se para a aritmética e a álgebra.
Só uma contagem especial, um
“número de vezes”, pode multiplicar outra contagem, seja esta de módulos ou
abstrata.
Uma expressão numérica pode ser
elevada ao quadrado? Depende. Por exemplo, uma medida geométrica sempre pode; a
massa de um corpo às vezes pode; uma contagem de módulos nunca pode.
Sobre expressões numéricas
A matemática é feita com expressões numéricas, não com números.
Peço observar, nas quatro multiplicações abaixo, que as expressões
numéricas entram nos cálculos, tanto nos dados como nas respostas, e não
somente os números:
3 x 3 = 9 (uma contagem abstrata é multiplicada)
3 x 3 livros = 9 livros (uma contagem de módulos é
multiplicada)
3 m x 3 m = 9 m² (duas medições se multiplicam)
3 m/s x 3 s = 9 m (duas grandezas da física se
multiplicam)
Sobre polinômio e
equação
O polinômio não é propriamente uma
igualdade, mas uma definição matemática feita por meio de uma soma algébrica de
contagens abstratas, nas quais há um “x” variável, isto é, um “x” que pode
assumir valores arbitrariamente escolhidos.
A equação é uma igualdade imposta a
duas somas algébricas, nas quais consta uma contagem desconhecida, “x”. Assim
entendida, a equação tem um único valor para “x”, ressalvado o caso
excepcional, o único que conheço, da equação do segundo grau, que discuto no Capítulo
IX.
Polinômios igualados a zero não dão
origem a equações e apenas indicam o ponto ou os pontos onde uma figura se
anula. São equações falsas, sem sentido e quase sempre insolúveis, ressalvados
apenas o caso da linha reta e o excepcional caso do trinômio do segundo grau.
Sobre a fórmula de
Bhaskara
A fórmula de Bhaskara, que permite
calcular as raízes de uma equação do segundo grau, é a recíproca matemática do
trinômio quadrado (y = ax²
+ bx + c). Quando se tratar de uma parábola, você pode escolher o caminho:
dado “x”, o trinômio calcula “y”;
dado “y”, a fórmula de Bhaskara
calcula o par de valores de “x” que lhe corresponde.
A fórmula de Bhaskara se aplica a
todos os pontos da parábola. E a nenhum ponto fora dela! Cuidado, pois, para
não criar “números imaginários”...
CAPÍTULO II - CONCEITO DE NÚMERO
Número é
uma ferramenta neutra e múltipla ao infinito, que serve para exprimir contagens
e aferições, em geral. As contagens podem ser de módulos ou abstratas.
Explicando ferramenta neutra e múltipla ao infinito
O número é
neutro, uma ferramenta sem nenhum sinal.
O número é
múltiplo ao infinito: há infinitos escaninhos, cada um com um número, a partir
de 1.
Não há
números positivos nem negativos nos infinitos escaninhos.
Explicando contagem de módulos
A contagem
de módulos é a soma algébrica, unidade por unidade, de uma dada quantidade de
módulos, ou seja, de “coisas” (100 laranjas). Subtrair uma contagem é o mesmo
que somar a imagem dessa contagem.
Uma
contagem de módulos multiplicada por um “número de vezes” tem outra contagem de
módulos como resultado.
(5 vezes
100 laranjas = 500 laranjas)
Uma soma
algébrica de contagens de módulos é também uma contagem de módulos.
(500
laranjas + 100 laranjas = 600 laranjas)
(500
laranjas - 100 laranjas = 400 laranjas)
Por ser uma
soma algébrica, uma contagem de módulos pode ser positiva ou negativa. Se
negativa, o sinal de “menos” é obrigatório na expressão quantitativa (- 500
laranjas).
A contagem
de módulos resulta num número seguido do módulo a que se refere: por exemplo,
uma conta bancária, que conta reais, pode ser, respectivamente, superavitária
(+ 100 reais) ou deficitária (- 100 reais).
Os sinais
de “mais” (+) e de “menos” (-) não são atributos dos números, mas das
contagens.
Explicando contagem abstrata
Enquanto
uma contagem de módulos especifica o que foi contado, a contagem abstrata
quantifica um avanço (ou recuo), como no caso da construção de uma figura, ou
um “número de vezes”, necessário a uma multiplicação.
Por ser uma
soma algébrica, a contagem abstrata no caso geral pode também ser positiva
(tradicional e impropriamente chamada de “número positivo”) ou negativa
(tradicional e impropriamente chamada de “número negativo”). Na prática, os
conceitos de número e contagem abstrata são tomados como indistintos, mas é
fundamental separar número “ferramenta” de número que exprime uma contagem,
porque aquele é neutro e apenas indicativo de quantidade (100), enquanto a
contagem, que é uma soma algébrica, construída passo a passo, pode ser positiva
(+100) ou negativa (- 100), indicando uma posição à frente ou atrás.
Os sinais
de “mais” (+) e de “menos” (-) não são atributos dos números, mas das
contagens.
As
contagens abstratas são usadas como multiplicadores de contagens ou de medições e no estudo dos polinômios e figuras.
Explicando as aferições
Medições,
pesagens e outras aferições são feitas por comparação com unidades físicas
arbitrariamente escolhidas, como o metro, o quilograma e o segundo. O resultado
de uma aferição é uma expressão numérica, com o número indicando quantas vezes
a unidade foi requerida na aferição.
Correlação com os esportes
O
número é o núcleo da expressão numérica de uma frequência, de uma posição, de
uma quantidade de módulos, de uma medição geométrica ou de uma aferição de uma grandeza
física.
A
esse respeito, cabe uma correlação da matemática com os esportes, vários deles
praticados com bola. Sem bola não há jogo. Cada modalidade esportiva tem:
-
Uma bola diferente: bola de futebol, bola de tênis, bola de voleibol, bola de
basquetebol;
- Regras diferentes.
O equivalente matemático da bola é a expressão numérica, sem a qual
também não há matemática. São as seguintes as expressões numéricas, com os
respectivos jogos matemáticos:
(1)
Contagens abstratas de frequências, isto é, de “números de vezes”: seus números
são usados nas multiplicações de contagens.
(2) Contagens
abstratas de avanços (posições): seus números são usados no estudo das funções e
no estudo de figuras.
(3)
Contagens de módulos: seus números são usados na aritmética da vida real e nas
equações que envolvem quantidades de módulos, isto é, de “coisas”.
(4)
Medições: seus números são usados na geometria e na física.
(5) Aferições
com unidades: seus números são usados na física.
Cada jogo
matemático tem a sua expressão numérica e suas regras para a utilização do
número que ela encerra. Por exemplo, contar, medir e pesar são operações de que
resultam expressões quantitativas diferentes, como: (a) 8; (b) 8 laranjas; (c)
8 metros; (d) 8 quilogramas.
Podemos
elevar essas expressões ao quadrado?
Para responder à questão, em cada caso temos de levar em consideração a
vinculação do número com a grandeza que está sendo quantificada:
(a) 8: a
resposta é sim, pois 8 é um número isolado
8 x 8 = 64
Estamos
falando aqui de números isolados.
b) 8
laranjas: a resposta é não, pois não há laranjas ao quadrado. As contagens de
módulos não podem ser submetidas a nenhuma potenciação ou radiciação.
Estamos
falando aqui de contagens de módulos.
(c) 8
metros: a resposta é sim, pois a geometria dá conta de que também existem
metros quadrados e metros cúbicos. Logo, a medida de uma distância pode ser
elevada ao quadrado e até ao cubo por autorização da geometria, mas a nenhuma
outra potência, inteira ou fracionária. A resposta é sim: 8 metros x 8 metros =
64 metros quadrados.
Estamos
falando aqui de medições.
Conforme
veremos no Capítulo VI, o metro é uma medida (uma unidade); o metro quadrado,
uma outra unidade, diferente da primeira; e o metro cúbico, uma terceira
unidade, diferente das anteriores. Logo, uma medição (em metros) pode ser
multiplicada por outra medição (em metros) para obter uma área (em metros
quadrados) e por uma área (em metros quadrados) para obter um volume (em metros
cúbicos).
(d) 8
quilogramas: a resposta é “depende”, pois o quilograma é a unidade de uma
grandeza física.
Estamos
falando aqui de ciência.
Nesse caso,
o quadrado é possível quando assim estabelecido em uma fórmula postulada pela
física, e não é possível em fórmulas que assim não o determinem.
Conforme
veremos no Capítulo VII, por autorização científica uma grandeza física pode
ser multiplicada pela mesma grandeza física ou por qualquer outra grandeza
física, desde que assim o determine a fórmula aplicável, sempre observando que
as unidades se envolvem nas operações, do que decorre uma nova unidade para o
resultado obtido.
Concluo
mencionando três exemplos de aplicação das expressões numéricas:
(1) no balanço contábil, que é um exercício de
álgebra, os números são fornecidos em reais e a resposta (lucro ou prejuízo) é
obtida em reais.
(2) no
cálculo de um volume, que é um exercício de geometria, os números são
fornecidos em metros e a resposta é obtida em metros cúbicos.
(3) no
cálculo da força que atua sobre um corpo, que é um exercício de física, a massa
é dada em quilogramas, a aceleração é dada em metros por segundo ao quadrado, e
a resposta é obtida em newtons.
Nos três
casos, os cálculos são feitos com os números-ferramenta, mas sob a égide das
expressões numéricas que eles quantificam, o que significa, em cada caso,
saber, por exemplo, se posso ou não fazer multiplicações, se posso ou não
elevar os dados ao quadrado ou como devo expressar o resultado da operação.
Tudo feito com o cuidado de observar o que acontece com as unidades.
Uma
alegoria do que ocorre nos esportes: é preciso respeitar as regras de cada
jogo.
A
multiplicação de contagens é um mecanismo que permite adicionar, na soma
algébrica, uma mesma contagem, positiva ou negativa, por um “número de vezes”
chamado de multiplicador.
O multiplicador, embora contagem, é
sempre neutro. Pois uma contagem “de vezes” é especial: nunca retrocede! Não há
um “número de vezes” negativo!
Nem tem sentido uma contagem
multiplicar um multiplicador!
É claro, portanto, que a ordem dos
fatores altera o produto! Três salas de vinte alunos dão sessenta alunos. Mas
vinte alunos vezes três salas não dão sessenta salas!
Uma contagem de módulos não pode,
igualmente, multiplicar outra contagem de módulos! Não posso multiplicar um
lucro no balanço por um saldo de gols, nem elevar uma dívida ao quadrado! Parece
um truísmo, e, não obstante, a observação é fundamental na matemática!
Essa a razão por que as equações
são do primeiro grau!
Multiplicação com dois
fatores negativos
A questão do produto com dois
fatores negativos só pode aparecer no âmbito das somas algébricas e dos
polinômios, onde a multiplicação com multiplicador aparentemente negativo
encobre na verdade a subtração de um produto negativo.
Ver que a contagem, seja abstrata,
seja de módulos, resulta de uma operação linear, no eixo das abscissas, a
partir de um ponto zero.
Logo, um “número negativo”, isto é,
uma contagem negativa, é a imagem de um “número positivo”, isto é, de uma
contagem positiva:
(- x) = - (+ x);
Um “número positivo”, por sua vez,
é a imagem de um “número negativo”:
(+ x) = - (- x).
Desse modo, um sinal
negativo corresponde à subtração de uma contagem positiva, tendo como resultado
uma contagem negativa. Dois sinais negativos equivalem à subtração de uma
contagem negativa, tendo como resultado uma contagem positiva.
Vejamos, pois, como proceder em
caso de dois fatores negativos.
Calcular (-7). (-5)
Apenas um dos fatores pode ser negativo, como
sabemos. Desse modo:
(-7). (-5) = - (7). (-5) = - (-35) = + 35
Trata-se, na verdade, da imagem de – 35. Um dos
sinais negativos indica que o produto é negativo. O outro indica que o que se
quer é a imagem desse produto negativo; portanto, o resultado é um número
positivo.
O mesmo raciocínio se repete, com alternância de
sinais, para potências maiores.
Calcular x³ para x = - 7
x³ = (-7). (-7). (-7) = - - (7) x (7) (-7) = - 343
Num desenvolvimento matemático, uma
contagem pode ser representada por uma letra: “a”, “b” et cetera, de maneira a
ter expressões literais do tipo (a + b + 85), (7 - a) e (A x B).
Quando se multiplicam duas
expressões literais ou no desenvolvimento de uma equação, pode-se chegar a uma
multiplicação com dois fatores negativos, como nos exemplos acima. Essa
multiplicação deve obedecer ao rationale anteriormente apresentado:
(-A) x (- B) = - (A) x (-B) = - (-AB) = +
(AB)
Exemplo:
(a-5) x (b-6) =
ab-6a-5b + (-5) x (-6) =
ab-6a-5b - (5) x (-6) =
ab-6a-5b -
(-30) =
ab-6a-5b + 30
Logo, (a-5) x (b-6) = ab-6a-5b + 30
Não se trata de (- 5) x (- 6), mas
da imagem de (5) x (-6) ou da imagem de (6) x (-5) = imagem de (-30) = + 30.
Multiplicar com dois fatores negativos só é possível no âmbito imbricado de
operações com expressões literais. O resultado é uma contagem positiva.
Observação: como sabemos,
multiplicações entre si de duas expressões literais somente são possíveis se se
referirem a medições ou a números isoladamente considerados.
Resolução do exercício anterior com
recursos da geometria
Seja calcular A1 = (x - a). (x – b)
Multiplicar (x - a) por (x - b) equivale a calcular a área de um
retângulo de lados (x- a) e (x - b), o que podemos fazer com o auxílio da
geometria.
Seja o quadrado de lado x, portanto de área A = x², como na
figura abaixo.
Desmembremos um dos lados desse quadrado em (x – a) e “a”, e o lado
adjacente, em (x – b) e “b”. O quadrado fica, na figura, dividido em quatro
retângulos, de áreas A1, A2, A3 e A4, de modo que:
A = A1 + A2 + A3 + A4
A = x²
A1 = (x - a). (x – b) = produto desejado
A2 = ax – ab
A3 = bx – ab
A4 = ab
A1 = A – A2 - A3- A4
A1 = x² - (ax –
ab) - (bx – ab) - ab
A1= x² - ax – bx + ab + ab – ab
A1 = x² - ax – bx
+ ab
Portanto,
(x- a). (x – b) = x² - ax – bx + ab
O produto (ab) resulta positivo a partir de uma soma algébrica de áreas
obrigada a ser igual a x², não porque “menos por menos dá mais”, embora esta expressão possa (e
deva) ser usada em caráter metafórico.
CAPÍTULO IV – POLINÔMIOS
O polinômio é uma soma algébrica em
que uma contagem abstrata, “x”, varia arbitrariamente, e é por isso chamada de
variável. A cada valor da variável “x”, temos o correspondente valor do
polinômio ou o ponto da figura gráfica que lhe corresponde.
O polinômio é uma definição
matemática, e não propriamente uma igualdade.
Veremos adiante que,
diferentemente, uma equação é um cotejo de duas somas algébricas de contagens,
obrigadas a serem iguais e no caso geral envolvendo uma única contagem
desconhecida, “x”, chamada de incógnita.
Um polinômio igualado a zero
torna-se uma falsa equação. Chama-se de raiz de um polinômio à abscissa de um
ponto que anula o polinômio. Como a figura correspondente pode fazer
revoluteios, a falsa equação pode ter mais de uma raiz ou nenhuma raiz. As
raízes de um polinômio de grau superior podem ser obtidas graficamente ou por
aproximações sucessivas. Entretanto, como exceção, um trinômio do segundo grau
igualado a zero pode ter suas raízes determinadas matematicamente, pela fórmula
de Bhaskara ou conforme apresento no Capítulo IX.
Um binômio algébrico corresponde à
linha reta; se multiplicarmos uma reta por outra temos um trinômio do segundo
grau; se multiplicarmos este por outra reta, um polinômio do terceiro grau; e
assim por diante, até chegar a um polinômio do enésimo grau. Igualado esse
polinômio a zero, resulta uma falsa equação, que se anula sempre que se anula
um dos n fatores, isto é, qualquer das “n” retas que o geraram. Tentar resolver
essa equação para encontrar as “n” raízes é um exercício matemático inútil, de
trás para frente, de quem está enxugando gelo. Ainda voltarei a esse ponto.
CAPÍTULO V -
MATEMÁTICA DAS CONTAGENS DE MÓDULOS
Paulo Silva tem 3
apartamentos, uma dívida bancária de 9.300 reais e 1.600 ações da Petrobras.
Essa informação contém três contagens, que não são contagens abstratas, mas
contagens de módulos, a saber, apartamentos, reais e ações. “Coisas”, enfim.
A contagem de
módulos, como a contagem abstrata de posições, resulta de somas algébricas de
contagens parciais simples ou de contagens agrupadas mediante a utilização de
um multiplicador.
O multiplicador é a
contagem de “um número de vezes”, e sabemos que nunca pode ser negativo.
Imagem
Tratando-se de uma
operação linear, com origem no ponto zero, uma contagem negativa de módulos, de
modo semelhante à contagem abstrata, é a imagem de uma contagem positiva de
módulos, em relação ao ponto zero:
Imagem de (+ x) = (- x)
Imagem de (- x) = -
(- x) = (+ x)
Multiplicação
Nenhuma das contagens
de módulos do Paulo Silva, mencionadas acima, pode ser elevada ao quadrado,
pois não existem apartamentos ao quadrado, reais ao quadrado ou ações ao
quadrado!
Consequência: toda
equação envolvendo módulos é do primeiro grau e tem uma única raiz.
CAPÍTULO VI - GEOMETRIA
A
geometria comporta-se, na sua relação com as medições, como se fosse um ramo da
ciência, impondo suas grandezas e gerando suas unidades derivadas. Com efeito,
a geometria das medições não trabalha com módulos, mas com três unidades, sendo
uma de comprimento, medida diretamente, e duas derivadas (por exemplo,
respectivamente, metro, metro quadrado e metro cúbico).
Medições diretas quantificam
segmentos de reta (em metros), produtos de dois segmentos de reta quantificam
áreas (em metros quadrados) e produtos de segmento de reta por área quantificam
volumes (em metros cúbicos).
Ver que na geometria uma medida
direta não pode ser elevada a nenhuma potência superior a três, nem a nenhuma
potência fracionária.
Além disso, não há equações na
geometria, cujas raras igualdades demonstram-se por recorrência aos teoremas,
como o teorema de Pitágoras: “num triângulo retângulo, o quadrado da hipotenusa
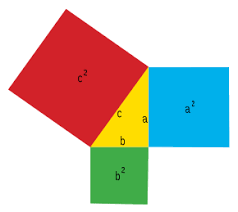
é igual à soma do quadrado dos catetos”.
|
25
|
|
5
|
|
5
|
|
4
|
|
4
|
|
3
|
|
3
|
|
a
|
|
b
|
|
c
|
|
|
|
9
|
|
16
|
Trata-se de uma igualdade
geométrica, uma fórmula imposta por um teorema geral da geometria, que não pode
ser confundida com uma equação, pois esta é uma imposição, caso a caso, da
igualdade de duas somas algébricas.
CAPÍTULO VII – CIÊNCIA
A
ciência, como a geometria das medições, define o que deve ser quantificado,
impõe a maneira de fazer mensurações e aferições, cria as unidades e propõe as
fórmulas onde usar as expressões numéricas.
Fórmulas
são definições matemáticas impostas pela ciência e suas leis.
Nelas se
indicam as operações matemáticas a serem realizadas, envolvendo nos cálculos
expressões numéricas de unidades. As unidades sofrem modificações resultantes
das interações requeridas pelas fórmulas. Por exemplo, um resultado expressando
newtons pode resultar de expressões fornecidas em metros e em quilogramas, como
na Lei da Gravitação Universal:
F = G (m1.m2) /r²
“No Universo tudo se passa como se
dois corpos se atraíssem com força proporcional às suas massas e inversamente
proporcional ao quadrado da distância que separa seus centros de
gravidade.”
A medida da
força da gravidade (F), em newtons, resulta do produto de um coeficiente gravitacional
G (em (newton.m²/kg²) pelo
quociente do produto das massas que se atraem (m1 e m2), em
quilogramas, pelo quadrado da distância que as separa (r²), em metros quadrados. Duas massas, em quilogramas, uma distância,
em metros, e um coeficiente gravitacional, com sua unidade, e uma resposta em
newtons.
CAPÍTULO VIII -
EQUAÇÕES
Equação é uma igualdade imposta a
duas somas algébricas, das quais consta um termo desconhecido, designado pela
letra “x” e chamado de incógnita.
Trata-se de uma igualdade
construída, podendo ser de módulos ou de números isolados (lúdica), que adiante
definiremos. Uma equação em que a incógnita é uma contagem de módulos tem de
ser necessariamente do primeiro grau porque não se pode multiplicar uma contagem
de módulos por outra e não se pode elevá-la a nenhuma potência. Desse modo, a
equação envolvendo módulos é sempre do primeiro grau e só pode ter uma raiz, a
incógnita “x” a ser descoberta.
“x” é uma contagem.
Método veneziano
A equação tem como
paradigma o “método veneziano”, também chamado de “método das partidas
dobradas”, justapondo duas somas algébricas de contagens construídas para serem
iguais. É o que fazem as empresas para apurar se houve lucro ou prejuízo nas
atividades do ano.
O que legitima a
equação impositiva é uma garantia de igualdade das duas somas algébricas, que
pode ser metodológica, como nas partidas dobradas da contabilidade e seus
balanços, ou estabelecida mediante confrontação de contagens sabidamente
equivalentes, como no exercício abaixo onde uma equação permite calcular a
idade com que o matemático Diofanto morreu, a partir da inscrição existente no
seu túmulo.

“Sua infância durou
um sexto da sua vida;
A senioridade veio um
doze avos depois;
um sétimo além,
contraiu núpcias;
seu filho nasceu
cinco anos depois;
esse filho, que era
fraco e doente, teve a metade da vida do pai;
e o pai, desgostoso,
sobreviveu apenas mais quatro anos.”
O recado no túmulo sugere
a seguinte equação:
x/6 + x/12 + x/7 + 5
+ x/2 + 4 = x
Preparando a equação,
temos:
9x = 756
x = 84 anos (idade
procurada)
Equações falsas
Uma equação falsa surge quando
arbitrariamente se iguala uma soma algébrica de contagens abstratas a zero.
Resolvê-la é encontrar os pontos onde se anula, um exercício ocioso e sem
perspectiva de êxito, observados apenas o caso da linha reta e o caso especial
do trinômio do segundo grau, conforme discuto no Capítulo IX.
As raízes de um polinômio igualado
a zero indicam pontos onde o polinômio se anula. Se a figura fizer 17
revoluteios em torno do eixo dos “x”, teremos 17 raízes cuja serventia é
indicar 17 pontos de ordenada nula. Resolver uma equação falsa é descobrir
esses pontos, um exercício despiciendo, com viés de insolúvel, com a ressalva
do caso da linha reta e do curioso caso da equação do segundo grau, em que as
raízes podem ser encontradas por meio da fórmula de Bhaskara.
Outro caso em que as raízes
realmente existem ocorre quando se iguala a zero um produto de “n” retas. Esse
produto, que é do grau “n”, se anula quando um dos fatores for nulo, o que
significa que se trata de uma falsa equação com “n” raízes, que são as raízes
das “n” retas. Nenhum interesse há em encontrá-las.
Seja, por exemplo, obter a (falsa)
equação do terceiro grau que corresponde à multiplicação dos três binômios a
seguir:
(y = x - 17), cuja raiz é 17;
(y = 2- x), cuja raiz é 2;
(Y = x + 1), cuja raiz é – 1.
Solução:
Produto: (x-17) (2- x) (x + 1) = x³ – 18x² + 15x + 34
(polinômio)
Falsa equação: x³ – 18x² + 15x + 34
= 0 (polinômio igualado a zero)
É evidente que a falsa equação
acima tem como raízes 17; 2; e (-1), cada uma anulando um dos fatores da
multiplicação que a originou. Resolver uma equação como essa é remar de trás
para a frente, um exercício inútil, de enxugamento de gelo.
O exemplo mostrou uma equação
falsa, cuidadosamente construída para ter três raízes. Imagine o leitor
encontrar as raízes, se houver, de uma equação falsa construída aleatoriamente!
Equação do segundo grau
Veremos no Capítulo IX o caso da equação
do segundo grau, que comporta uma excepcionalidade: pode ser considerada falsa
ou verdadeira.
De
fato, um trinômio do segundo grau igualado a zero dá origem a uma equação do
segundo grau falsa, de contagens. Veremos que esta equação coincide com uma
equação verdadeira, de números: ou seja, a mesma equação será falsa ou
verdadeira, conforme seja o objetivo pretendido pelo operador matemático. É
como na física quântica, onde a luz pode ser onda ou partícula, alternando-se
de acordo com a experiência conduzida pelo observador.
Suas duas incógnitas (quando verdadeira) ou suas duas raízes (quando falsa) podem ser encontradas utilizando a fórmula de Bhaskara.
Equações lúdicas
Equações lúdicas são equações que envolvem números isoladamente considerados, e não contagens de módulos ou abstratas. Por exemplo, é lúdica a equação que resolve a seguinte questão: achar três números consecutivos cuja soma é 153.
Por que chamar de lúdicas essas equações? Porque a princípio o interesse nessas equações é apenas recreativo, sem aplicação na vida real. Qual a utilidade de encontrar números que não significam nada? De saber que os números solicitados são 50, 51 e 52?
Uma equação envolvendo números pode ser de qualquer grau, desde que resulte de uma igualdade imposta a duas somas algébricas. Entretanto, não é fácil construir igualdades verdadeiras de somas algébricas com incógnitas de grau superior a um. Se for possível construí-la, outro problema será resolvê-la.
Equações na ciência
A ciência trabalha com unidades,
não com módulos, e de acordo com fórmulas impostas caso a caso. A famosa
equação de Einstein, e = m.c², é um postulado
científico, e não verdadeiramente uma equação, ou seja, não é um confronto de
duas igualdades construídas para encontrar uma quantidade desconhecida.
Não me atrevo a dizer que a ciência não tem equações, mas tenho para mim que a Lei da
Gravitação Universal, a Equação de Clapeyron, a Segunda Lei de Newton, a Lei de Coulomb, tanto quanto as Equações de Campo de Einstein, são imposições científicas, e não equações.
CAPÍTULO IX – A EQUAÇÂO
QUE PODE SER FALSA OU VERDADEIRA
A Física Quântica nos ensina que a luz pode comportar-se como onda ou como partícula, dependendo da experiência que estiver sendo conduzida pelo observador.
A Física Quântica nos ensina que a luz pode comportar-se como onda ou como partícula, dependendo da experiência que estiver sendo conduzida pelo observador.
Por exemplo, quando se faz incidir luz ultravioleta sobre uma chapa metálica, a luz, comportando-se como partícula, choca-se com os elétrons do metal e produz o efeito fotoelétrico. Isaac Newton decretou: a luz é partícula, pois só uma partícula desloca outra partícula, como uma bola de bilhar chocando-se contra outra.
Se, em vez disso, a luz incide sobre um anteparo com duas fendas próximas, a luz passa ao mesmo tempo pelas duas fendas. Foi por isso que Christiaan Huygens concluiu que a luz é uma onda, pois só uma onda poderia realizar essa façanha, a de passar ao mesmo tempo em dois lugares diferentes.
Quem estava com a razão?
Ambos, decidiu Einstein mais de duzentos anos depois, pois a luz a um só tempo é partícula e onda.
Ou seja, a natureza tem dois modelos, dos quais, percebendo um, fica o observador impedido de perceber o outro. Dois modelos e um só aspecto! Uma ordem explicada e uma ordem implicada!
Algo assim ocorre na matemática, com a equação do segundo grau, que pode ser falsa, de contagens, ou verdadeira, lúdica, conforme pretendo mostrar a seguir.
A falsa equação do segundo grau: sem enredo
Vimos que um polinômio igualado a zero dá origem a uma falsa equação envolvendo contagens. Um exemplo, sem dúvida, é o do trinômio do segundo grau, y = ax² + bx + c, correspondente a uma parábola, que, igualado a zero, dá origem a uma equação com duas raízes, que não são incógnitas, mas os pontos onde a parábola corta o eixo das abscissas.
Trata-se de uma equação de contagens, o que significa que x² = x*.x, em que x* é multiplicador e x, a incógnita, com x* e x tendo o mesmo valor numérico. Esta é a única equação de contagens por mim conhecida que não é do primeiro grau, com a importante observação de que é uma falsa equação, destinada a localizar pontos.
A curva tem dois ramos simétricos
que se iniciam no vértice “V”, de abcissa x = - b/2a, que, no caso da figura, é
o ponto de mínima ordenada do trinômio. Um ponto qualquer, no ramo esquerdo da
parábola, como o ponto “C” da figura, tem obviamente ordenada igual à do
ponto que lhe é simétrico no ramo direito.
Ver que as raízes, “x1” e “x2”, são igualmente pontos simétricos da parábola.
Ver que as raízes, “x1” e “x2”, são igualmente pontos simétricos da parábola.
Igualado o trinômio a zero, temos uma equação falsa, cujas raízes, “x1” e “x2”, podem ser calculadas usando a fórmula de Bhaskara:
x1 e x2 = (-b ± √ (b² - 4ac)) /2a
Mas a fórmula de Bhaskara não se aplica apenas aos pontos em que y = 0. Aplica-se a todos os pontos da parábola! Para cada valor de “y” da parábola, como o do ponto “C”, podem ser calculados os dois correspondentes valores de “x” com auxílio da fórmula.
Dado um valor qualquer de “y” = y*, diferente de zero, a equação se altera, substituindo “c” por “ c´ ”, em que c’ = c – y*. Aplicando-se a fórmula de Bhaskara com “ c’ ” no lugar de “c”, obtêm-se os dois valores, “x1” e “x2”, correspondentes ao “y*” dado e ao seu simétrico.
Fórmula de Bhaskara para qualquer y = y*:
x1 e x2 = (-b ± √ (b² - 4ac’)) /2a, em que c’ = c – y*.
Ou seja, a milenar fórmula de Bhaskara, que os matemáticos usam para extrair as raízes da equação do segundo grau, é na verdade a recíproca do trinômio, isto é, dado “x”, o trinômio calcula “y”; dado “y*”, Bhaskara calcula os dois valores correspondentes de “x1” e “x2”. A variável dependente passa a independente, e vice-versa!
Obviamente, quando y* = 0, “x1” e “x2”” tornam-se as raízes do trinômio.
Bhaskara não dá certo quando “y*” é menor que “yV”, pois nesse caso “y*” não pertence à parábola: Bhaskara desemboca nesse caso em uma raiz quadrada de um número negativo, o que não é possível na matemática. Um valor de “y*” menor do que “yV” só existe imaginariamente.
Exercício
Calcular os dois valores de “x” da parábola definida pelo trinômio quadrado (y = x² - 5x + 6), correspondentes aos seguintes pontos:
y* = 0;
y* = 2;
y* = 10;
y* = - 3
Primeiro caso y* = 0
x² - 5x + 6 = 0
c´= c – 0 = 6
x1 e x2 = (5 ± √ (5² - 4x6)) / 2: 2 e 3
Trata-se das duas raízes do trinômios, ou seja, os dois pontos onde a parábola se anula.
Segundo caso y* =2
x² - 5x + 6 = 2
c´ = 6-2 = 4
x² - 5x + 4 = 0
x1 e x2 = (5 ± √ (5² - 4 x 4) / 2: 1 e 4
Trata-se de dois pontos simétricos da parábola.
Terceiro caso y*=10
x² - 5x + 6 = 10
c´= 6 – 10 = - 4
x² - 5x - 4 =0
x1 e x2 = (5 ± √ (5² + 4 x 4)) / 2: - 0,7 e 5,7
Trata-se de dois pontos simétricos da parábola.
Quarto caso y*= -3
x² - 5x + 6 = - 3
c´ = 6 – (- 3) = 9
x² - 5x + 9 = 0
x1 e x2 = (5 ± √ (5² - 4x9)) / 2 = (5 ± √ (-11)) / 2 (operação impossível).
É impossível extrair a raiz quadrada de um número negativo (-11), o que significa que y* = -3
não é ordenada de nenhum ponto da parábola em questão.
De fato,
Trinômio: y = x² - 5x + 6
Derivada primeira do trinômio: y´ = 2x – 5
2 xmin - 5 = 0
xv = xmin = 2,5,
yv = (2,5² - 5 x 2,5 + 6) = - 0,25.
Portanto, nenhum ponto da parábola tem um y* menor que - 0,25. Ou seja, y* = - 3 não pertence à parábola.
A verdadeira equação do segundo grau: com
enredo
Vejamos agora o que acontece quando procuramos resolver a seguinte proposição: calcular dois números cuja soma é 5 e cujo produto é 6.
Esse enunciado nos leva a multiplicar “x” por (5-x) e igualar o resultado a 6, ou seja, a construir uma equação lúdica:
(x). (5 -x) = 6 (dois
membros obrigados a serem iguais)
ou
5x – x² = 6 (uma equação do segundo grau).
Preparando a equação acima para aplicar a fórmula de Bhaskara, temos:
x² – 5x + 6 = 0
Trata-se de uma equação lúdica, porque foi construída com números, e não com contagens, pois, com estas, (x) não poderia multiplicar (5 -x). É, além disso, uma equação verdadeira, pois corresponde a uma igualdade imposta. Não a um polinômio igualado a zero.
Coincide com a
equação falsa do trinômio igualado a zero!
Uma só equação com duas funções matemáticas distintas: pois uma coisa é buscar, dos infinitos pontos de uma parábola, os dois pontos em que o trinômio se anula; outra, muito outra, é calcular dois números cuja soma é 5 e o produto é 6.
Claro que em ambos os casos os dois números procurados são 2 e 3, obtidos usando a fórmula de Bhaskara. São, a um só tempo, as duas incógnitas da equação e as duas raízes que anulam o trinômio, a indicar os dois pontos onde a parábola encontra o eixo das abscissas num gráfico cartesiano.
Como calcular as incógnitas (ou raízes), sem
utilizar Bhaskara
Para resolver a equação do segundo grau sem utilizar Bhaskara, temos de usar um artifício: calcular “YV”, o mínimo “Y” da parábola, o que exige derivar o trinômio e obter “xmin”, o ponto do qual equidistam as duas raízes:
xmin = - b/2a
x1 = xmin – d
x2 = xmin + d
Com os valores de “xmin” e de “d”, obtêm-se as raízes, “x1” e “x2”.
Exemplo:
Resolver a equação x² - 5x + 6 = 0
xmin = -b/2a = 2,5
Pode-se calcular “d” tanto com auxílio de “x1” quanto de “x2”.
A) - Escolhamos inicialmente substituir “x” por x2= 2,5 + d
x2²- 5x2 + 6 = 0
x2 = 2,5 + d
(2,5 + d)² – 5 (2,5+ d) + 6 = 0
(2,5² + 5d + d²) – 12,5 - 5d + 6 = 0
6,25 + d² – 6,5 = 0
d² = 0,25
d = 0,5
Portanto:
x1 = 2,5 – d = 2
x2= 2,5 + d = 3
B) – Repitamos o desenvolvimento, mas substituindo “x” por x1= 2,5 - d
(2,5 – d)² - 5 (2, 5 - d) + 6 = 0
(2,5² - 5d + d²) – 12,5 + 5d + 6 = 0
6,25 + d² – 6,5 = 0
d²= 0,25
d = 0,5
Portanto:
x1= 2,5 – d = 2
x2= 2,5 + d = 3
Um exercício
interessante é examinar os desenvolvimentos em A e B acima e observar como a
matemática ajusta suas parcelas para corresponder ao fato de que, em relação a xmin, o desvio de x2 e o desvio de x1 são iguais e
simétricos (- d) e (+ d), respectivamente).
Em A:
(2,5² + 5d + d²) – 12,5 - 5d + 6 = 0,
ou 6,25 + d² – 6,5 =
0
Em B:
(2,5² - 5d + d²) – 12,5 + 5d + 6 = 0,
ou 6,25 + d² – 6,5 =
0
Dois caminhos e um só resultado: 6,25 + d² – 6,5 = 0.
Poderosa matemática...







